Perché topologia

Da parecchi anni ho scelto di fare con i miei alunni un po’ di topologia, prima di tornare a parlare di triangoli, quadrati e quant’altro, per diversi motivi.

Innanzitutto la topologia mi piace, mi piace tanto. E sono convinta che insegnare ciò che ci piace sia (certamente un privilegio, ma anche) un dovere. Perché solo quando insegnamo ciò che ci appassiona possiamo essere davvero credibili.

Inoltre la topologia spiazza e dunque permette con facilità di catturare l’attenzione degli alunni, di tutti gli alunni. La topologia stupisce, perché nel giro di pochissimo si passa dal mettersi d’accordo sul significato che diamo a certe parole al vedere risultati non banali, inaspettati, quasi magici (e stupisce non solo i ragazzini: provate a tagliare un nastro di Möbius in sala insegnanti…!).

Non da meno, la topologia permette di staccarsi dalle proprietà metriche delle figure, sulle quali a volte si insiste talmente tanto da far sembrare la geometria solo un ambiente in cui esercitarsi sulle quattro operazioni.

Tau topologo

Insomma, quest’anno sto per incominciare nel solito modo (che comprende la costruzione e il taglio di una serie di nastri per contarne facce e bordi, un gioco con dei palloncini per osservare la deformazione delle figure e poi alcuni problemi a partire da Il problema delle cinque camere), quando per motivi che non sto a raccontare qui ^[1] mi imbatto in Tau topologo. La fiaba che racconta la matematica superiore ai bambini scritta da Franco Ghione.

Il primo giorno di scuola leggo ad alta voce in classe le prime pagine del primo capitolo, dove si racconta La storia del signor Tau. I ragazzi ascoltano in silenzio: è incredibile il potere di una bella storia.

Il nastro di Möbius

Leggo fin dove si dice che il signor Tau ha in casa una scultura di gesso che rappresenta un nastro di Möbius, “l’esempio più semplice di superficie non orientabile”. Ci fermiamo e ciascuno di noi costruise con due striscette di carta una superficie cilindrica e un nastro di Möbius, per toccare con mano che cosa significhi “superficie non orientabile”. Nell’ora successiva, con una collega di Arte e immagine che deve fare un’ora di supplenza in quella classe, colorano i nastri.

Il gioco dell’isola

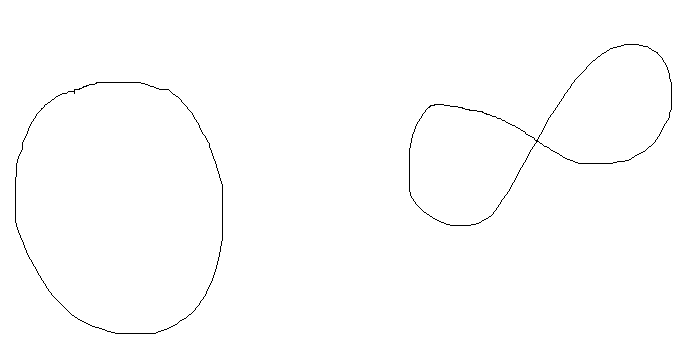
Vorrei soffermarmi ancora sui nastri di Möbius, per studiarli un po’ meglio, per tagliarli, per farne con ulteriori avvolgimenti, ma la collega di arte mi dice di avere un’altra ora di supplenza in giorno dopo e mi chiede di lasciarle del lavoro da far fare ai ragazzi. Così, il secondo giorno di scuola, racconto brevemente che cosa accadeva nella casa del signor Tau e perché spesso si riempisse di bambini; spiego alla classe che cosa si intenda per curva chiusa semplice, disegnando alla lavagna col gesso una linea che assomiglia ad un ovale e una che assomiglia ad un otto: una curva chiusa semplice e una curva chiusa intrecciata.

È mia intenzione introdurre quello che in Tau topologo è chiamato Il gioco dell’isola, per andare a lavorare su il “dentro” e il “fuori” della curva, ma per il momento tengo nello zaino curve più complicate, che ho portato per far loro colorare nell’ora successiva “l’isola” e “il mare”, e chiedo ai ragazzi di disegnare su un foglio tre curve chiuse semplici, giusto per assicurarmi di avere tutti in testa la stessa idea.

Una sola alunna non sa da che parte partire; mi dà l’impressione che la richiesta le sembri troppo facile rispetto alle solite, perché mi basta ripeterla senza nemmeno cambiare tanto le parole, che ha già disegnato sul foglio le sue tre curve. Giro tra i banchi per assicurarmi che tutto sia chiaro e…

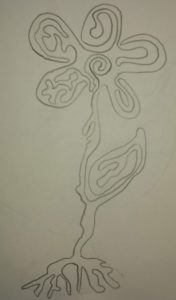
Pensavo di essere io a stupire i miei alunni con la topologia ed invece, come spesso accade, sono loro a stupire me. Come sia venuto in mente a Yibo, dopo aver visto il mio uovo e il mio otto, di disegnare questo topo e questo fiore, per me è un mistero.
Un mistero bellissimo.

Il dentro e il fuori

E allora, senza dover saltare di palo in frasca, sono proprio le curve disegnate da Yibo che ci fanno rendere conto che non è sempre facilissimo capire se un punto sta nella regione di piano che sta “dentro” la curva chiusa o in quella che sta “fuori” la curva.

Consegno a ciascuno una copia di questo disegno di Robert Bosh, che avevo trovato il giorno prima grazie a Base cinque di Gianfranco Bo.

Chiedo a ciascuno di scegliere un punto sul proprio foglio e di chiedersi se sta dentro o fuori la curva. Rispondere sembra impossibile, la maggior parte di loro ride divertita. Bastano pochi istanti a Giuseppe per dire: “Basta che seguiamo la strada dal punto che abbiamo colorato in avanti e vediamo se si arriva fuori, prima o poi. Se si arriva fuori vuol dire che anche il punto è fuori.” Non sarà proprio detta bene, ma tutti hanno capito e allora la mia richiesta è stata questa: “Colorate tutta la regione del foglio al quale appartiene il punto che avete scelto”.

L’ora è finita presto, ma per “dare loro un lavoro da fare” durante la lezione successiva, ho lasciato altre curve, fotocopiate da Tau topologo: non vedo l’ora di andare a scuola per vedere come hanno colorato le regioni!

Note

[1] A consigliarmi la lettura di Tau topologo (o meglio a consigliarmi di farlo leggere a mio figlio) è stata la professoressa Maria Dedò, ordinario di geometria che negli ultimi anni anni si è occupata in particolare di comunicazione e divulgazione della matematica e che ho avuto la fortuna di conoscere grazie ai corsi MathUp. Se avessi la dote della sintesi, riuscirei brevemente a raccontare perché siamo arrivate a parlare di  Tau topologo, ma siccome non ce l’ho, so che ne verrebbe fuori un altro articolo. Sarebbe un’altra storia bella da raccontare, che ancora direbbe quanto i ragazzini possono essere profondi e possono stupirci nella loro capacità di cogliere aspetti non banali degli enti (topologici, geometrici, matematici…) che man mano incontrano.