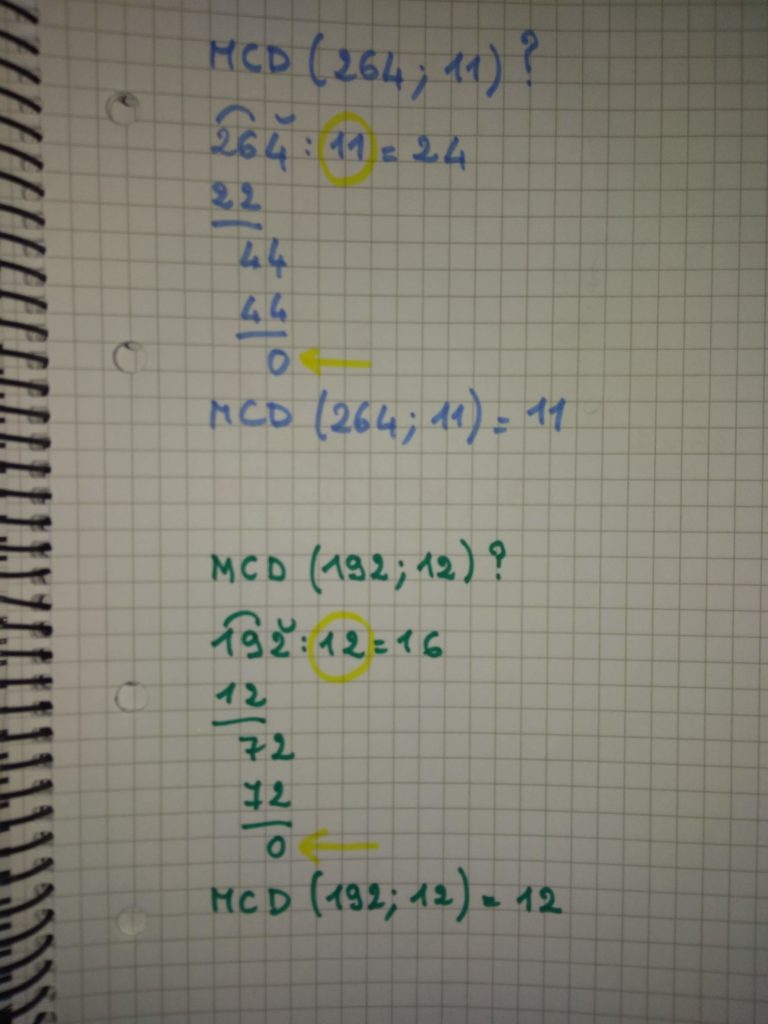Ricerca del MCD con il metodo di Euclide delle divisioni successive
Cercare il massimo comun divisore (MCD) tra due numeri naturali è cercare il più grande numero naturale che è sottomultiplo sia del primo che del secondo numero.
Fin qui non abbiamo detto nulla rispetto a come fare per trovare il MCD: abbiamo semplicemente ridetto la stessa cosa con parole leggermente diverse, che forse ci possono far capire meglio come sia venuta ad Euclide l’idea di procedere per divisioni successive.
Immaginiamo di voler preparare due passatoie, ossia due tappeti lunghi e stretti, di una lunghezza prefissata, a partire da dei pezzi rettangolari, tutti uguali tra loro e il più lunghi possibile.
Possiamo trovarci in tante situazioni diverse che, come vedremo, possono però essere ricondotte tutte ad un unico “modello”.
Quando il MCD è il più piccolo dei due numeri
Può succedere che se prendiamo un pezzo lungo esattamente come il tappeto più corto, questo “ci stia” un numero esatto di volte in quello più lungo.
In questo caso basterà fare dei pezzi tutti uguali al secondo tappeto: il secondo tappeto sarà allora formato da un unico pezzo e quello lungo da un certo numero di pezzi uguali al secondo.
Con i numeri la situazione è analoga.
I “tappeti” illustrati nel disegno qui sopra, potrebbero corrispondere a questa situazione: cerco il MCD (18 ; 6). Se mi accorgo subito che 18 è un multiplo di 6, allora subito posso dire che
MCD (18 ; 6) = 6.
Se non mi accorgo (perché magari i numeri sono più grandi), mi basta provare a fare la divisione tra il più grande dei due numeri e quello più piccolo: se il resto della divisione è 0, significa che il più piccolo dei due numeri è già il MCD tra i due numeri dati.
Esempi
Quando basta un ulteriore passettino
Un pezzo lungo come il tappeto più corto, però, potrebbe anche non starci un numero esatto di volte in quello più lungo. In questo caso dobbiamo un po’ ragionare per capire che cosa fare.
Se siamo fortunati, la parte che avanza al tappeto più lungo dopo aver accostato tanti pezzi lunghi come il tappeto più corto, ci sta un numero intero di volte nel tappeto più corto (e quindi anche in quello più lungo): avremo così trovato quanto cercavamo.
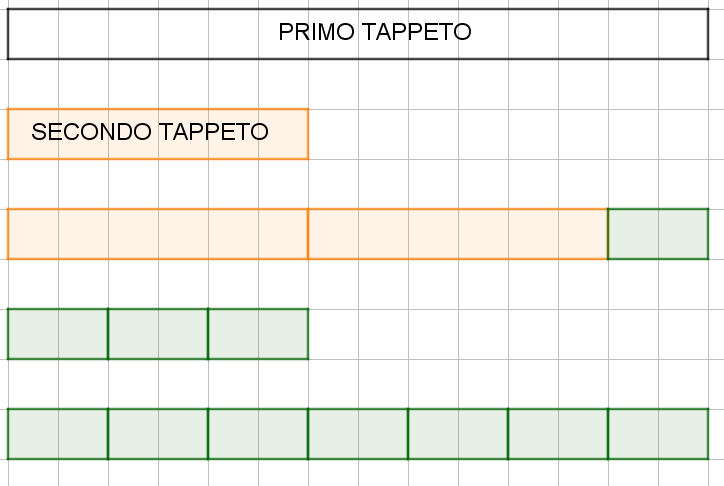
I “tappeti” illustrati nel disegno qui sopra, potrebbero corrispondere a questa situazione: cerco il MCD (14 ; 6).
6 non è un divisore di 14: il 6 nel 14 ci sta 2 volte, ma poi ho il resto di 2.
Sono fortunato perchè questo resto (2) divide esattamente il 6 e quindi
MCD (14 ; 6) = 2
Esempi
Un caso particolare
Un caso particolare molto semplice è quello che si presenta quando il resto della divisione tra il numero più grande e quello più piccolo è 1, ossia quando i due numeri sono uno il successivo dell’altro.
In questo caso è ovvio che il massimo comun divisore tra i due sarà proprio 1.
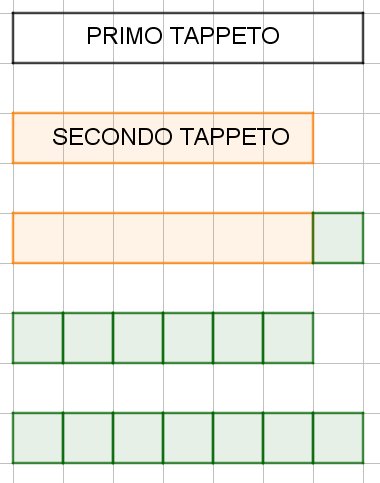
I “tappeti” illustrati nel disegno qui sopra, potrebbero corrispondere a questa situazione: cerco il MCD (7 ; 6).
6 non è un divisore di 7: il 6 nel 7 ci sta 1 volte, ma poi ho il resto di 1.
Ovviamente questo resto (1) divide esattamente anche il 7 e quindi
MCD (7 ; 6) = 1
Ma senza fare alcun calcolo, se abbiamo capito il senso di quello che stiamo facendo, potremo dire che
MCD (567 ; 566) = 1
MCD (45678 ; 45679) = 1
MCD (123456 ; 123457) = 1
Quando bisogna armarsi di pazienza
Potrebbe anche succedere che un pezzo lungo come il “resto” della divisione tra il tappeto più lungo e quello più corto, però, non stia un numero esatto di volte in quello più corto (e quindi nemmeno un quello più lungo). In questo caso però possiamo continuare a ripetere lo stesso procedimento, fino a quando non troveremo un “resto” che divide esattamente il pezzo più corto fino ad allora considerato: quel pezzo sarà quello cercato.
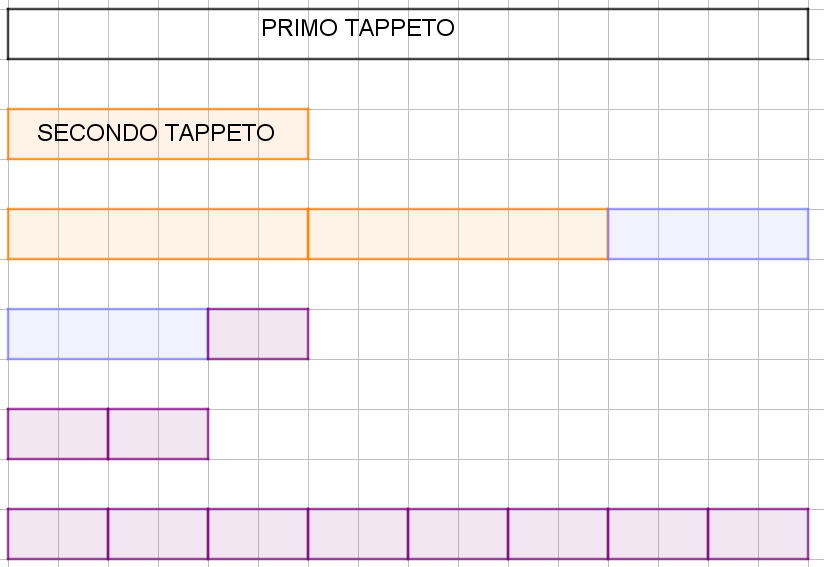
I “tappeti” illustrati nel disegno qui sopra, potrebbero corrispondere a questa situazione: cerco il MCD (16 ; 6).
6 non è un divisore di 16: il 6 nel 16 ci sta 2 volte, ma poi ho il resto di 4.
E 4 non è un divisore di 6: il 4 nel 6 ci sta 1 volta, ma poi ho il resto di 2.
Questo resto (2), però, divide esattamente il 4, il 6 e il 16 e quindi possiamo dire che
MCD (16 ; 6) = 2