I pattern dei multipli di 3
In classe, lavorando in gruppi, avete colorato i multipli di 3 in diversi schemi.
Abbiamo poi, insieme, osservato questo:
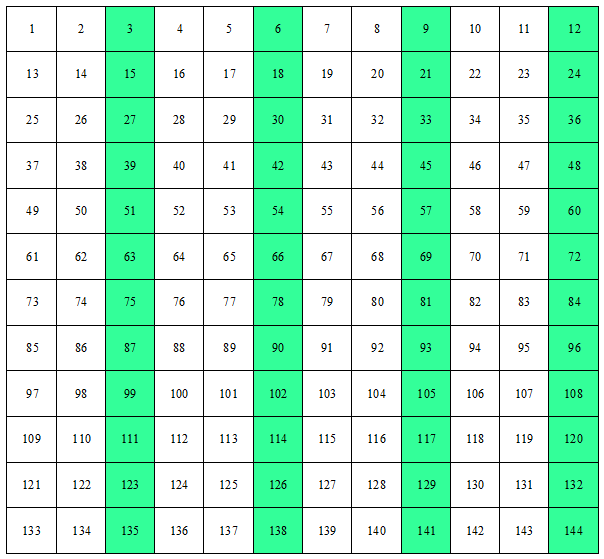
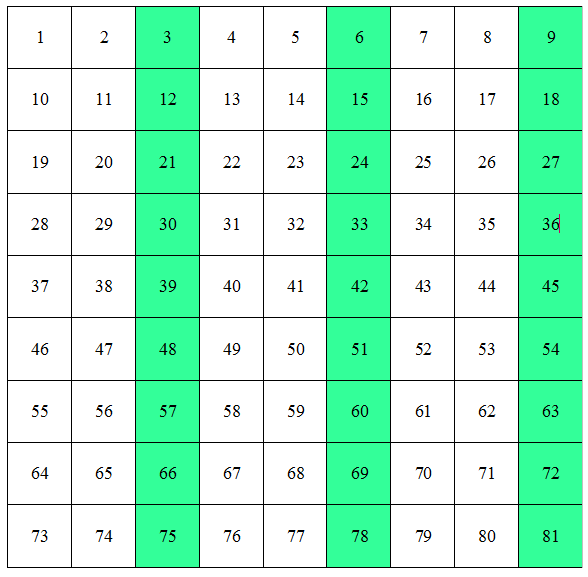
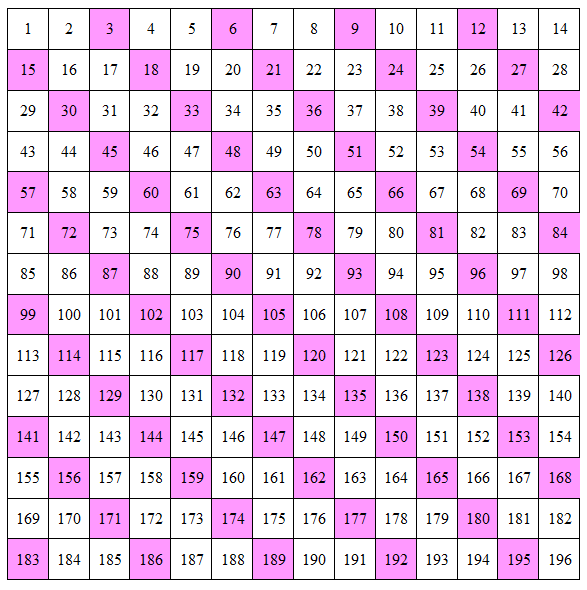
In questo schema i numeri naturali sono inseriti in successione, partendo da 1; in ogni riga ci sono 12 numeri. I multipli di 3 risultano messi in striscie verticali. Vi ho chiesto: quali altri potrebbero essere i numeri contenuti nella prima riga affinché i multipli di 3 siano sempre in striscie verticali? Alcuni di voi, a ragione, hanno detto che questo accade ogni volta che l’ultimo numero della prima riga è un multiplo di 3. Le stesse striscie verticali si presentavano infatti nello schema che aveva 30 numeri per riga e si presentano in quest’altro schema, che ha 9 numeri per riga (12, 30 e 9 sono multipli di 3).
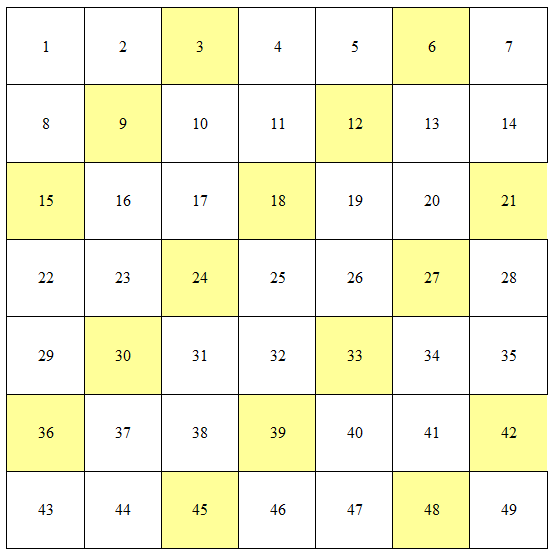
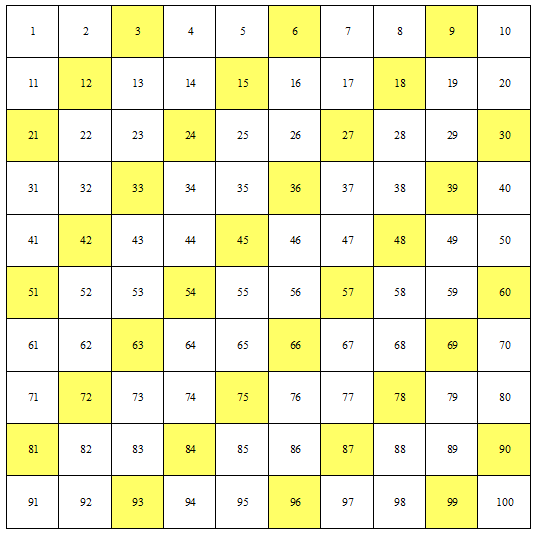
In classe abbiamo poi osservato questi altri due schemi:
Anche in questi schemi i numeri naturali sono inseriti in successione, partendo da 1; in ogni riga del primo ci sono 7 numeri, in ogni riga del secondo ce ne sono 10. I multipli di 3 risultano messi in file che qualcuno di voi ha caratterizzato con l’espressione [sinistra 1, giù 1] che ricorda quelle che noi abbiamo usato per il coefficiente angolare delle rettee che sta a significare che se parti da un quadretto colorato, vai a sinistra di 1 e scendi di 1, trovi un altro quaderetto colorato.
Vi ho chiesto: quali altri potrebbero essere i numeri contenuti nella prima riga affinché i multipli di 3 siano sempre disposti in questo modo? Alcuni di voi hanno detto che questo accade ogni volta che l’ultimo numero della prima riga NON è un multiplo di 3. Ma io non sono d’accordo. E per sostenere la mia ragione ti faccio vedere quest’altro schema, che in classe non abbiamo visto, ma che è quello a cui ho pensato per dire che non ero d’accordo:
Anche in questo schema i numeri naturali sono inseriti in successione, partendo da 1; in ogni riga ci sono 14 numeri. Anche 14 non è un multiplo di 3, eppure i multipli di 3 risultano messi in file che non seguono la stessa inclinazione di quelle degli schemi che ho colorato in giallo. Potremmo caratterizzare le file di quadratini colorati con l’espressione [destra 1, giù 1] che ricorda quelle che noi abbiamo usato per il coefficiente angolare delle rette e che sta a significare che se parti da un quadretto colorato, vai a destra di 1 e scendi di 1, trovi un altro quaderetto colorato.
La domanda è: posto che se l’ultimo numero della prima riga è un multiplo di 3, tutti i multipli di 3 risultano messi in striscie verticali (come negli schemi colorati di verde), quando invece l’ultimo numero della prima riga NON è un multiplo di 3, c’è modo di sapere come risultano disposti tutti i multipli di 3?
In altre parole: se l’ultimo numero della prima riga NON è un multiplo di 3, c’è modo di sapere (guardando solo questo ultimo numero) se i multipli di 3 saranno disposti con coefficiente angolare [sinistra 1, giù1] o [con coefficiente angolare destra 1, giù1]?
In altre parole ancora: se l’ultimo numero della prima riga NON è un multiplo di 3, c’è modo di sapere (guardando solo questo ultimo numero) se i multipli di 3 saranno disposti su file come quelle degli schemi colorati in giallo o su file come quelle dello schema colorato in rosa?
E se proprio poi volete esagerare: in schemi di questo tipo (cioè con i numeri naturali inseriti in successione partendo da 1), è possibile che i multipli di 3 siano messi in qualche modo diverso (sempre a seconda di quale è l’ultimo numero della prima riga), che non sia come quelli verdi, né come quelli gialli, né come quello rosa?