Quinto allenamento in vista dei Campionati
Ecco il quinto allenamento on-line di questo anno per tutti gli alunni della scuola “Piero Calamandrei” di Chirignago che desiderano allenarsi per la semifinale dei Campionati Internazionali di Giochi Matematici. Aspetto le vostre risposte: potete consegnarmele a scuola, su un foglietto, o inviarmele per posta elettronica all’indirizzo
sofia.sabatti@comprensivocolombo.it
(se le scriveste tra i commenti qui sotto, rischiereste di “spoilerare”, e non sarebbe bello…)! Non dimenticatevi di indicarmi anche il vostro nome e il vostro cognome.
Pesci e pescatori
Enrico e Dario amano pescare. Un giorno vanno a pesca insieme, entrambi accompagnati dal proprio figlio.
Enrico pesca tanti pesci quanti ne pesca suo figlio.
Dario pesca il triplo dei pesci pescati da suo figlio.
In totale hanno pescato 35 pesci.
Quanti pesci ha pescato ciascun pescatore?
Il figlio di Enrico si chiama Alvise.
Come si chiama il figlio di Dario?

(liberamente tratto da Eduardo Veloso e Josè Paulo Viana, Desafios 4. Problemas e histórias da matemática no público, edições Afrontamento, 1995)
Risposte al quarto allenamento in vista dei Campionati
Ho ricevuto tre risposte al problema “La corsa delle bandierine“, nessuna delle quali è del tutto corretta (ma ciascuna delle quali contiene qualche buona idea).
Se sei tra coloro che non sono riusciti a risolvere il gioco delle bandierine, non scoraggiarti! Forse ho esagerato con la difficoltà: sarebbe potuto andare bene per qualche categoria più avanzata rispetto a quelle cui appartengono gli studenti della scuola media. Ho voluto metterlo perché, a mio parere, se la soluzione è difficile da trovare, è anche facile da capire (quando qualcuno te la mostra) e, capìta una volta, la si può usare in tante altre situazioni.
Vediamo un po’ di spiegare come si può fare.
Tutte le risposte che ho ricevuto propongono (o come soluzione, o come tentativo) il considerare di mettere le bandierine nel punto medio dei lati del campo, così:
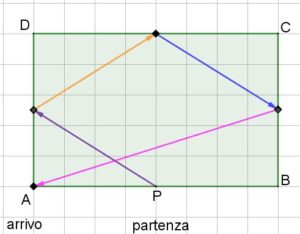
Applichiamo ora una serie di “riflessioni successive” al rettangolo ABCD e ai vari tratti di percorso in essi segnati, così:
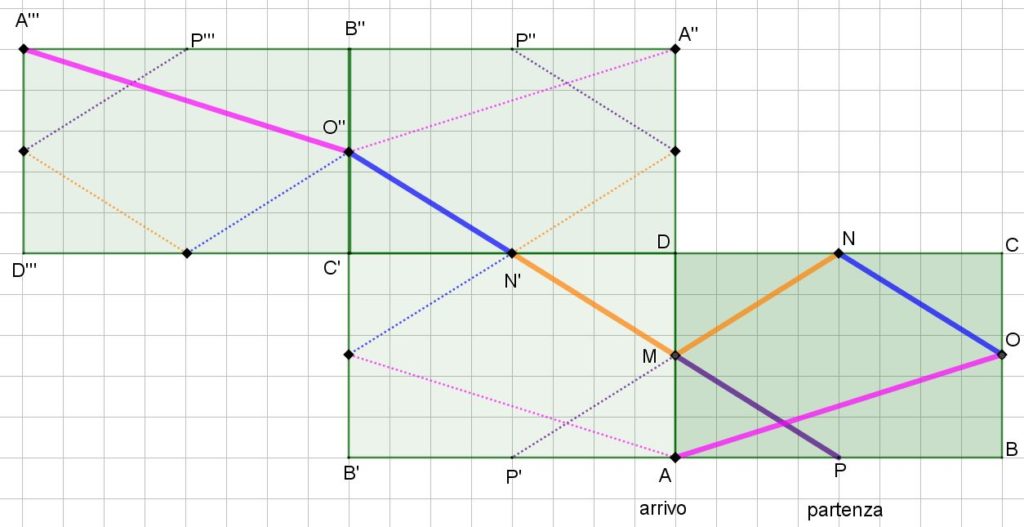
Sei d’accordo sul fatto che la lunghezza del percorso PM+MN+NO+OA è esattamente uguale alla lunghezza del percorso PM+MN’+N’O”+O”A”’?
Se non sei d’accordo, guarda meglio e rifletti!
Ecco, adesso probabilmente sarai d’accordo!
Prova ora a confrontare il percorso rosso (il segmento PA”’) con il percorso a zig zag che abbiamo visto prima.
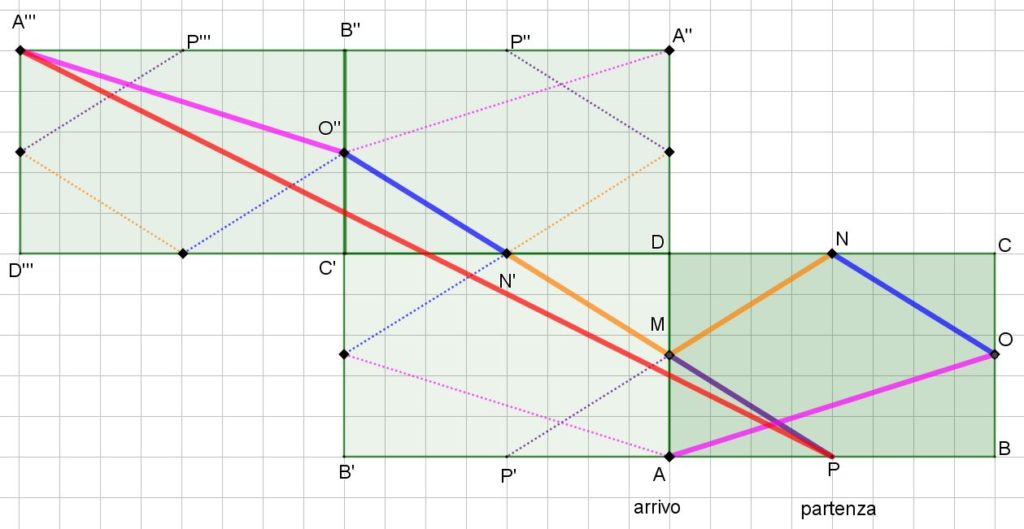
Sei d’accordo sul fatto che la lunghezza del percorso PA”’ è minore di quella del percorso PM+MN’+N’O”+O”A”’?
Se non sei d’accordo, guarda meglio e rifletti!
Ti chiedo di più: sei d’accordo sul fatto che il percorso rosso è la via più breve per andare da P ad A”’?
Credo che tu non abbia grossi dubbi: lo sai da quando eri piccolo che il percorso più corto per andare da un punto ad un altro è il segmento di retta che li congiunge!
Il problema è che noi non vogliamo andare da P ad A”’, ma da P ad A, passando per gli altri lati del campo.
Proviamo a fare a ritroso lo stesso procedimento che abbiamo fatto prima con i segmenti PM, MN, NO ed OA.
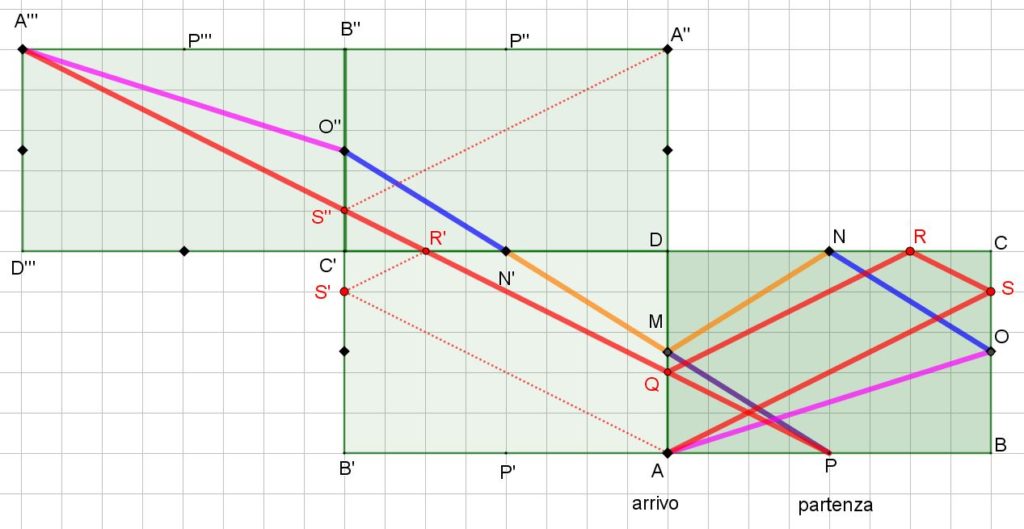
Sei d’accordo sul fatto che la lunghezza del percorso PA”’=PQ+QR’+R’S”+S”A”’ è esattamente uguale a quella del percorso PQ+QR+RS+SA?
E sei d’accordo sul fatto che se PA”’ è la via più breve per andare da P ad A”’ allora il percorso PQ+QR+RS+SA è quello più breve tra tutti quelli che ci permettono di andare da P ad A toccando prima gli altri lati del campo?
Che cosa abbiamo imparato?
Credo che questo problema metta bene in luce un fatto molto importante (parto da 7, perché 6 cose le abbiamo già imparate commentando i primi due allenamenti).
7. Se non puoi andare dritto, trova un modo di raddrizzare il tutto!
Per risolvere questo problema (ed altri simili: tipicamente molti problemi che riguardano il tavolo da biliardo) di fatto occorre sapere solo due cose: che la via più breve per andare da un punto a un altro è il segmento di retta, e che le isometrie (in questo caso la riflessione, ma in altri casi potrebbe essere la rotazione, o la traslazione, o la glissoriflessione) non cambiano le distanze.
Non ci sono altre cose da sapere. Serve però trovare un modo utile per usare queste due informazioni al nostro scopo!

