Quarto allenamento
Innanzitutto complimenti agli aspiranti campioni che hanno già risolto il terzo quesito: Laura Fronte (classe 2a A), Chiara Olivio (classe 2a C), Beatrice Da Lio (classe 1a A), Riccardo Falcier (classe 1a A), Pietro Cazzago (classe 1a D), Roberto Signoretto (classe 1a D), Anna Ceroni (classe 2a C), Luca Antonello (classe 2a C), Marco Cinquegrani (classe 2a C), Beatrice Bolognato (classe 3a C), Emma Sofia Zanin (classe 3a B), Ilenia Defina (classe 2a C), Andrea Sartori (classe 2a C), Ambra Vanessa Zottino (classe 2a C).
Ho ricevuto un po’ meno risposte rispetto a quelle che mi avete mandato per i primi due quesiti: spero sia solo un caso, o che siate stati impigriti dal fatto che dovevate consegnarmi anche il disegno (mannaggia alla proverbiale pigrizia dei matematici!)
In ogni caso, vedetevela con questa strana ruota. Sappiate che è un quesito considerato da 3 punti (quelli che abbiamo visto fin ora valevano 1 o 2 punti).
Dai Campionati internazionali di giochi matematici: la ruota di Matilde (Parigi, 1 settembre 2001)
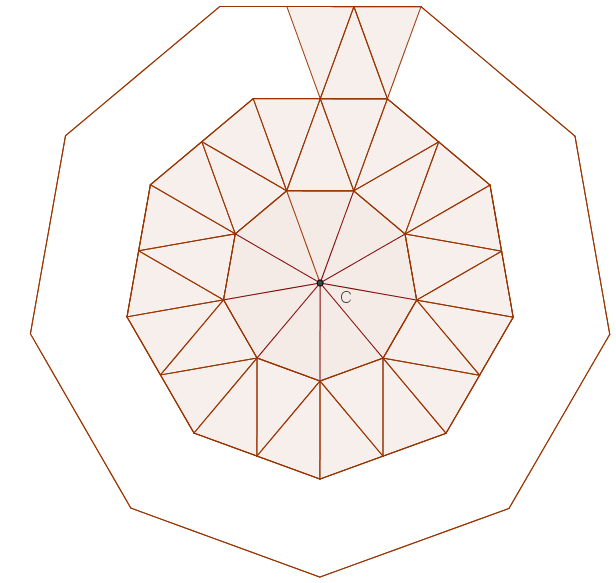
Matilde vuole ricoprire una superficie con dei triangoli isosceli tutti uguali tra loro.
Incomincia col disporre nove triangoli intorno al punto C, come in figura.
Poi circonda questi nove triangoli con una corona di altri triangoli, sempre come in figura.
Poi decide di aggiungere una seconda corona, il cui perimetro esterno è indicato dalla linea.
Quanti triangoli avrà utilizzato Matilde in totale quando avrà finito?
Aspetto le vostre soluzioni entro le ore 23:59 del 17 febbraio 2017. Speditemele per posta elettronica, non come commento qui sotto, altrimenti chi vede il vostro commento si rovina il gusto di giocare.
Usando i commenti potete, invece, farmi domande o chiedere spiegazioni!
“Una grande scoperta risolve un grande problema, ma c’è una briciola di scoperta nella soluzione di qualsiasi problema. Il tuo problema può essere semplice, ma se mette alla prova la tua curiosità e mette in gioco le tue capacità di invenzione, e se tu lo risolvi con i tuoi mezzi, puoi provare la tensione e il trionfo della scoperta. Queste esperienze possono creare un gusto per il lavoro intellettuale e lasciare la loro impronta sulla mente e sul carattere per tutta la vita.” (George Polya)